机器学习(1)
前言
吴恩达机器学习回顾使用
介绍
什么是机器学习
对于机器学习的两种定义:
- “the field of study that gives computers the ability to learn without being explicitly programmed.” - Arthur Samuel
- “A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.” - Tom Mitchell
任何机器学习问题可以归于两大类之一:监督学习(Supervised Learning),或无监督学习(Unsupervised Learning,或称非监督学习)。当然,还有半监督学习、强化学习等,尚不在讨论范围内。
监督学习
监督学习使用有标签的数据集,其任务是学习一个模型,使模型能够对任意给定的输入,对其相应的输出做出一个好的预测。
监督学习问题被分为**回归(Regression)和分类(Classification)**问题:
- 回归问题:将输入变量映射到某个连续函数,即预测一个连续值;
- 分类问题:将输入变量映射到离散的类别中,即预测一个离散值。
无监督学习
在无监督学习中,使用的数据集没有标签,不知道结果会是什么样子,但可以通过聚类的方式从数据中提取一个特殊的结构。
模型和成本函数
模型表示
为了描述监督学习问题,我们的目标是,通过一个训练集,学习一个函数 $h : X \rightarrow Y$,使得 $h(x)$ 对于对应值 $y$ 是一个很好的预测器。由于历史原因,$h(x)$ 被称为假设函数(hypothesis function)。
成本函数
**成本函数(cost function)**用于测量假设函数的准确度,即模型预测的好坏:
$$J(\theta_0, \theta_1) = \frac{1}{2m}\sum^m_{i=1}(\hat y_i - y_i)^2 = \frac{1}{2m}\sum^m_{i=1}(h_{\theta}(x_i) - y_i)^2$$
这个函数也被称为“平方误差函数(Squared error function)”或者“均方误差(Mean squared error)”。在取平均时多了一个 $\frac{1}{2}$,这是为了方便计算梯度下降,求导时 $\frac{1}{2}$ 将被消掉。
参数学习
梯度下降
在已有假设函数和成本函数的情况下,用**梯度下降(Gradient Descent)**可以估计得到假设函数中的参数。迭代使用:
$$\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta_0, \theta_1)$$
直到收敛或到达预定的迭代次数。
其中,$j = 0,1$ 表示特征的 index,$\alpha$ 为学习率。
多元线性回归
引入多元
引入以下符号:
- $x_j^{(i)}$:第 $i$ 个训练样本的特征 $j$ 的值
- $x^{(i)}$:第 $i$ 个训练样本的所有特征
- $m$:训练样本的数量
- $n$:特征的数量
则有多项式的假设函数:
$$h_{\theta}(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3 + … + \theta_n x_n$$
令 $x_0 = 1$,则上式可以简写为:
$$h_{\theta}(x) = \big[\theta_0\ \ \theta_1\ \ … \ \ \theta_n\big] \left[\begin{matrix}x_0\\ x_1\\ …\\ x_n\end{matrix}\right]= \theta^Tx$$
对于多元的梯度下降
同理,有
$$\theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta)$$
当 n >= 1 时,有
$$\frac{\partial}{\partial \theta_j}J(\theta) = \frac{1}{m}\sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})x^{(i)}_j$$
注意以上等式由
$$J(\theta) = \frac{1}{2m}\sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})^2$$
推得。
实践中的梯度下降 - 特征缩放
可以通过使每个输入值在大致相同的范围内来加速梯度下降。这是因为梯度在小范围内下降快,而在大范围内下降较慢;另外,对于不平整的变量,梯度在下降至最优值的过程中会出现降低效率的震荡。
因此将**特征缩放(feature scaling)和均值归一化(mean normalization)**两种技术结合使用。特征缩放将输入值除以输入变量的范围(即最大值减去最小值),从而得到一个大小为 1 的新范围;均值归一化涉及从输入变量的值减去输入变量的平均值,从而导致输入变量的新平均值为 0。公式为:
$$x_i := \frac{x_i - \mu_i}{s_i}$$
其中,$\mu_i$ 是特征 $i$ 所有值的平均值,$s_i$ 是特征 $i$ 的范围(最大值减最小值)。
实践中的梯度下降 - 学习率
当学习率 $\alpha$ 太小,则梯度下降太慢;而当学习率 $\alpha$ 太大,则梯度可能不会下降,也因此不会收敛。因此有时需要观察并进行调整。
参数计算
正规方程
梯度下降是最小化 $J$ 的一种方法。第二种方法是正规方程(Normal Equation),它显式地执行最小化,而不使用迭代式的算法。
$$\theta = (X^TX)^{-1}X^Ty$$
正规方程方法中,无需做特征缩放。两种方法的对比如下:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要选择学习率 |
| 需要多次迭代 | 不需要迭代 |
| $O(kn^2)$ | $O(n^3)$,需要计算 $(X^TX)^{-1}$ |
| 当 n 较大时效果很好 | 当 n 较大时速度较慢 |
不过正规方程方法要求 $X^TX$ 可逆。$X^TX$ 不可逆的原因有两种可能:
- 列向量线性相关:即训练集中存在冗余特征(特征线性依赖),此时应该剔除掉多余特征;
- 特征过多(多于样本数量):此时应该去掉影响较小的特征,或引入正则化(regularization)项。
正规方程的推导过程
把数据集表示为矩阵
$$X = \left( \begin{matrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{md} & 1 \\ \end{matrix} \right) = \left( \begin{matrix} x_{1}^T & 1 \\ x_{2}^T & 1 \\ \vdots & \vdots \\ x_{m}^T & 1 \\ \end{matrix} \right)$$
同时将标签也写成向量形式
$$y = (y_1;y_2;…;y_m)$$
由均方误差最小化,可得
$$\theta^* = arg_{\theta}min(y-X\theta)^T(y-X\theta)$$
其中,$\theta^*$表示 $\theta$ 的解。
令
$$E_{\theta} = (y-X\theta)^T(y-X\theta)$$
对 $\theta$ 求导得到
$$ \begin{equation} \begin{split} \frac{\partial E_{\theta}}{\partial \theta}&=-X^T(y-X\theta) + (y^T - \theta^TX^T) \cdot (-X)\\ &=2X^T(X\theta - y) \end{split} \end{equation} $$
令上式为 0,有
$$2X^T(X\theta - y) = 0$$
$$X^TX\theta = X^Ty$$
最终得到
$$\theta = (X^TX)^{-1}X^Ty$$
当 $X^TX$ 不为满秩矩阵(不可逆)时,可解出多个 $\theta$ 使均方误差最小化。因此将由学习算法的归纳偏好来决定选择哪一个解作为输出,常见的做法就是引入正则化项。
Logistic Regression
二分类
$$h_{\theta} = g(\theta^Tx)$$
$$z = \theta^Tx$$
$$g(z) = \frac{1}{1 + e^{-z}}$$
其中,$g(z)$ 被称为 Sigmoid 函数(或者 Logistic 函数),将任意实数映射到 (0, 1) 区间。这样,可以通过划分判定边界(decision boundary)进行分类。
成本函数
Logistic Regression 不能使用和线性回归相同的成本函数,因为 Sigmoid 函数是非凸的,容易陷入局部最优。
作为替代,使用以下成本函数:
$$J(\theta) = \frac{1}{m}\sum^m_{i=1}Cost(h_{\theta}(x^{(i)}), y^{(i)})$$
$$Cost(h_{\theta}(x), y) = -y log(h_{\theta}(x)) - (1-y)log(1-h_{\theta}(x))$$
注意,$y$ 只有 0 或 1 两种取值。
向量化的表示为:
$$h = g(X\theta)$$
$$J(\theta) = \frac{1}{m} \cdot (-y^Tlog(h) - (1-y)^Tlog(1-h))$$
梯度下降
由梯度下降的一般形式:
$$\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j}J(\theta)$$
可以推导出 LR 的梯度下降公式:
$$\theta_j := \theta_j - \frac{\alpha}{m} \sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})x_j^{(i)}$$
向量化表示为:
$$\theta := \theta - \frac{\alpha}{m}X^T(g(X\theta) - \vec y)$$
推导过程如下:
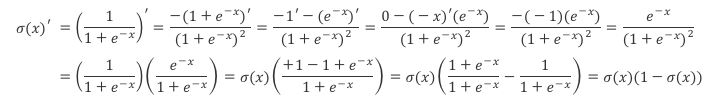

正则化
**高偏差(high bias)或者欠拟合是指模型对已有数据的拟合较差,通常因为模型太简单或者使用过少的特征;而高方差(high variance)**或者过拟合是指模型对已有数据的拟合过强,以至于对于新数据无法很好的预测,通常因为模型过于复杂。
两种技术可用于处理过拟合问题:
- 减少特征数量:人工选择留下的特征,或者使用特征选择的算法;
- 正则化(Regularization):留下所有的特征,但是减小参数 $\theta_j$。
加入正则化的成本函数
$$min_{\theta}\frac{1}{2m}\Big[\sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda \sum^n_{j=1}\theta_j^2\Big]$$
其中,$\lambda$ 用于控制参数过大所付出的代价。$\lambda$ 选取过大时,可能导致欠拟合。
加入正则化的线性回归
梯度下降
$$\theta_0 := \theta_0 - \alpha \frac{1}{m}\sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})x_0^{(i)}$$
$$\theta_j := \theta_j - \alpha \Big[\Big(\frac{1}{m}\sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})x_j^{(i)} \Big) + \frac{\lambda}{m}\theta_j \Big] \ \ \ \ j = 1, 2, …, n$$
正规方程
$$\theta = (X^TX + \lambda \cdot L)^{-1}X^Ty$$
$$where \ L= \begin{bmatrix} 0 & & \\ & 1 & \\ & & \ddots \\ & & & 1 \end{bmatrix}$$
加入正则化的 Logistic Regression
成本函数
$$J(\theta) = -\frac{1}{m}\sum^m_{i=1}\Big[y ^{(i)}log(h_{\theta}(x^{(i)})) + (1-y^{(i)})log(1-h_{\theta}(x^{(i)}))\Big] + \frac{\lambda}{2m}\sum^n_{j=1}\theta^2_j$$
梯度下降
$$\theta_0 := \theta_0 - \alpha \frac{1}{m}\sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})x_0^{(i)}$$
应用机器学习的建议
决定下一步做什么
模型的预测错误可以通过以下方式进行排解:
- 更多训练数据:解决高方差
- 用更少的特征:解决高方差
- 用额外的特征:解决高偏差
- 用多项式特征:解决高偏差
- 增大或减小正则化参数 $\lambda$:解决高方差或高偏差
可以通过画出**学习曲线(Learning curves)**来帮助分析。
模型选择和训练、验证、测试集
假设函数可能在训练集上拟合得很好,但是由于过拟合,在实际使用中表现不佳。因此,我们将数据集划分为训练集、验证集和测试集,以评估假设函数。
- 验证集:对应在训练中不断更新的参数和模型准确率;
- 测试集:对应超参数和最终的模型准确率。
或者说,验证集用于模型选择和调参,而测试集用于估计实际使用时的泛化能力。这样,我们不需要在利用测试集调参后,又使用测试集来估计泛化能力而得到错误的结果。
诊断偏差和方差
偏差(欠拟合):
- $J_{train}(\theta)$ 较高;
- $J_{train}(\theta) \approx J_{train}(\theta)$。
方差(过拟合):
- $J_{train}(\theta)$ 较低;
- $J_{train}(\theta) \geq J_{train}(\theta)$。
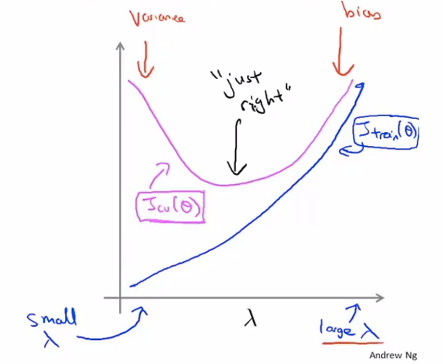
正则化和偏差、方差
$$J(\theta) = \frac{1}{2m}\sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m}\sum^m_{j=1}\theta_j^2$$
首先考虑不使用正则化,然后选取一系列想要尝试的 $\lambda$ 值,最小化代价函数来得到 $\theta$,然后用验证集来评估,评估时用的代价函数去掉正则项:
$$J_{cv}(\theta) = \frac{1}{2m_{cv}}\sum^{m_{cv}}_{i=1}(h_{\theta}(x^{(i)}_{cv}) - y_{cv}^{(i)})^2$$
可以画一幅如下图所示的图像来确定合适的 $\lambda$(实际一般有噪声):
机器学习系统设计
误差分析
可以将误分类的验证集数据提出来,看看哪一类误分类比例最高,做出相应的改进。
不对称性分类的误差评估
当正负样本的比例比较悬殊时,单纯使用正确率来评估会使得分类器只预测一种结果。因此,我们可以使用**准确率(Precision)和召回率(Recall)**作为评估度量。
$$P = \frac{TP}{TP+FP}$$
$$R = \frac{TP}{TP+FN}$$
两者都较高,说明模型在面对偏斜类时也有很好的表现。但大部分情况下,需要在两者之间做权衡。如果想要结果要较高的确信度,那么将准确率作为最重要的标准;如果不想漏掉样例(例如疾病判断),那么将召回率作为最重要的标准。
如果想要综合评价,我们可以使用 F1-Score:
$$F1 = \frac{2PR}{P+R}$$
支持向量机
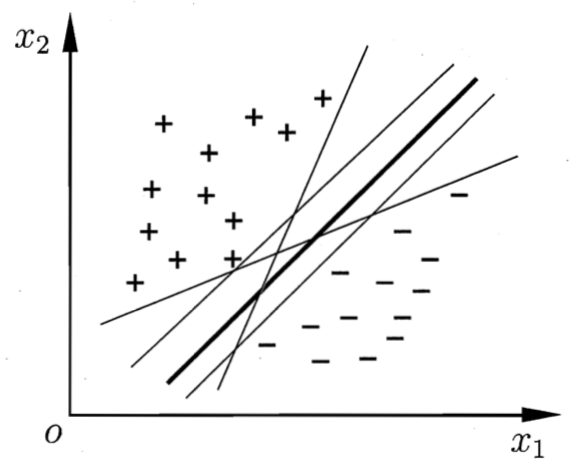
直观理解
支持向量机(Support Vector Machine),便是根据训练样本的分布,搜索所有可能的线性分类器中最佳的那个。因为决定直线位置的并非所有的训练数据,而是其中的两个空间间隔(margin)最小的两个不同类别的数据点,这种可以用来真正帮助决策最优线性分类模型的数据点叫做支持向量(support vector)。
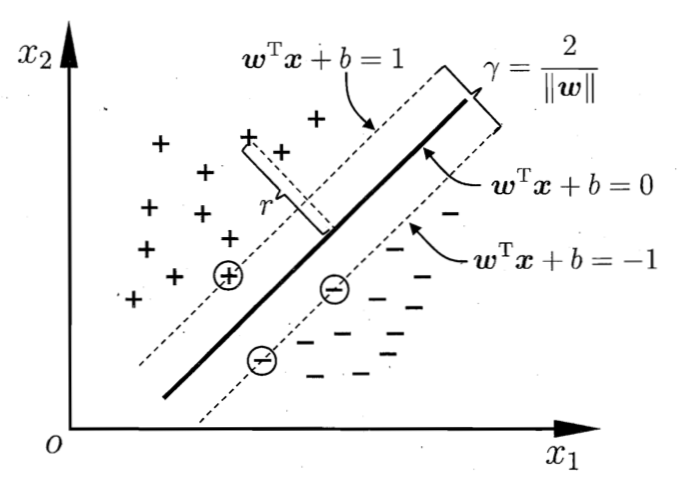
数学原理
在样本空间中,划分超平面可通过以下线性方程来描述:
$$w^Tx+b = 0$$
其中,$w = (w_1;w_2;…;w_d)$ 为法向量,决定了超平面的方向;$b$ 为位移项,决定了超平面与原点之间的距离。显然,划分超平面 $(w, b)$ 可被法向量 $w$ 和位移 $b$ 确定。
样本空间中任意点 $x$ 到超平面 $(w,b)$ 的距离可写为
$$r=\frac{|w^Tx+b|}{\|w\|}$$
假设超平面 $(w,b)$ 能将训练样本正确分类,即对于 $(x_i, y_i) \in D$,若 $y_i = +1$,则有 $w^Tx_i+b>0$;若 $y_i = -1$,则有 $w^Tx+b < 0$。令
$$ \begin{equation} \begin{cases} w^Tx_i+b \geq +1, & y_i=+1 \\ w^Tx_i+b \leq -1, & y_i=-1 \end{cases} \end{equation} $$
总存在缩放变换使得上式成立。可以理解为构造了一个安全间距。
显然,支持向量使得上式中的等号成立。它们到超平面的距离之和即间隔,为
$$\gamma = \frac{2}{\| w \|}$$
我们的目标是找到具有最大间隔的划分超平面,即找到满足 $y_i(w^Tx_i+b) \geq 1, i = 1, 2, …, m$ 的参数 $w$ 和 $b$,使得 $\gamma$ 最大,即等价于最小化 $\frac{1}{2}\| w \|^2$。
核函数
思想
可以用带有**核函数(kernal)**的支持向量机构造复杂的非线性分类器。我们需要定义一个类似于度量相似性的函数,以高斯核函数为例:
$$ \begin{equation} \begin{split} f_1 &= similarity(x, l^{(1)}) \\ &= exp \Big( -\frac{\| x-l^{(1)} \|^2}{2\sigma^2} \Big) \\ &= exp \Big( -\frac{\sum^n_{j=1}(x_j - l^{(1)}_j)^2}{2\sigma^2} \Big) \end{split} \end{equation} $$
其中,$\sigma^2$ 是高斯核函数的参数。当 $x$ 约等于 $l^{(1)}$ 时,$f_1$ 约等于 1;而当 $x$ 和 $l^{(1)}$ 较远时,$f_1$ 约等于 0。
通过相似度函数,$l_1$,$l_2$,… ,$l_j$ 每一个标记会定义一个新特征 $f_1$,$f_2$,…,$f_j$。假设有 $\theta_0 + \theta_1 f_1 + \theta_2 f_2 + … + \theta_j f_j \geq 0$,我们由此将复杂的非线性决策边界转换为线性。
选取标记点
每个标记点都和每个样本点位置重合,即 $l^{(m)} = x^{(m)}$。则有
$$f_m^{(i)} = sim(x^{(i)}, l^{(m)})$$
$$f^{(i)} = [f_0^{(i)}, f_1^{(i)}, … ,f_m^{(i)}]^T$$
$f^{(i)}$ 就是特征向量。
因此,包含核函数的 SVM:
给定 $x$,计算出特征 $f \in \mathbb{R}^{m+1}$,当 $\theta^Tf \geq 0$ 时,预测 $y = 1$。则目标为
$$min_{\theta}C\sum^m_{i=1}\Big[ y^{(i)}cost_1(\theta^Tf^{(i)}) + (1-y^{(i)})cost_0(\theta^Tf^{(i)}) \Big] + \frac{1}{2}\sum^m_{j=1}\theta^2_j$$
一个数学细节是 $\sum_j \theta^2_j$ 可以被写为 $\theta^T \theta$(忽略 $\theta_0$)。而在实现时,通常用 $\theta^T M\theta$,$M$ 是一个依赖于所使用的核函数的矩阵,这是一种略有区别的距离度量方法。这使得 SVM 的实现更有效率。
核函数的思想可以用于例如 Logistic 回归的其他分类器,但是运行十分缓慢,不能使用高级优化技巧。
参数选择
对于参数 $C$,其作用近似于 $\frac{1}{\lambda}$。
- 较大的 $C$:意味着不使用正则化,低偏差高方差
- 较小的 $C$:偏向于欠拟合,高偏差低方差
$\sigma^2$:
- 偏大时:特征 $f_i$ 更为平滑,高偏差低方差
- 偏小时:特征 $f_i$ 更不平滑,低偏差高方差
使用 SVM
使用 SVM 时,需要确定参数 $C$ 和核函数。
可以不使用核函数,也称使用线性核函数,则 $\theta^Tx \geq 0$。当特征数目较多而样本数较少时,这样可以避免去在一个非常高维的空间中拟合过于复杂的非线性函数,减缓过拟合。
当特征数目较少而训练样本较多时,想用核函数拟合相当复杂的非线性决策边界,高斯核函数是个不错的选择。如果决定使用高斯核函数,还需要选择 $\sigma^2$。
如果有大小很不一样的特征变量,在使用高斯核函数前,要注意将特征变量大小按比例归一化。
最常用的两个核函数是线性核函数和高斯核函数。不是所有提出来的相似性函数都是有效的,需要满足默塞尔定理(Mercer’s Theorem),使得用于求解 $\theta$ 的数值优化技巧能够使用。
其他可以使用的核函数有:
- 多项式函数(Polynomial kernel):$k(x, l) = (X^Tl + m)^n$。通常效果较差,常用于 $x$ 和 $l$ 都是严格的非负数。
- 字符串核函数(String kernel):用于输入数据是字符串时。
- 卡方核函数(chi-square kernel)
- 直方相交核函数(histogram kernel)
如何选择使用 Logistic 回归还是 SVM?
- 当特征数量远大于训练样本数,一般使用 Logistic 回归,或使用线性核函数的 SVM。
- 当特征数量较少,训练样本数中等时,一般使用带高斯核函数的 SVM。
- 当特征数量较少,训练样本数非常多(一般大于十万),一般先增加更多特征变量,然后使用 Logistic 回归或者使用线性核函数的 SVM。
而设计较好的神经网络可能能获得较好的效果,但训练速度较慢。并且 SVM 的优化是一种凸优化问题,不会有困扰神经网络的局部最优问题。
无监督学习
在监督学习中,我们有一系列标签,然后用假设函数去拟合它。作为对比,在无监督学习中,数据不带有标签。我们通过这些数据找到一些隐含在数据中的结构。聚类算法是一种典型的无监督学习算法。
K-Means 算法
K-means 是一种经典的聚类算法,其需要的输入包括聚类数目 $K$ 和训练集 $\big\{x^{(1)}, x^{(2)}, …, x^{(m)}\big\}$。
步骤:
- 随机初始化 $K$ 个聚类中心 $\mu_1, \mu_2, …, \mu_K \in \mathbb{R}^{n}$;
- 将训练集中的每个数据点分配给离它最近的聚类中心,最终形成 $K$ 个聚类;
- 对于每个聚类,将聚类中所有数据点的平均点作为新的聚类中心;
- 重复第 2 步和第 3 步直到收敛。
可能在过程中出现没有任何数据点的聚类中心,这种情况下一般直接移除,或者如果确实需要 $K$ 个聚类,则可以重新随机初始化一个聚类中心。
优化目标
规定下列符号:
- $c^{(i)}$:$x^{(i)}$ 被分配给的聚类的序号;
- $\mu_k$:第 $k$ 个聚类中心;
- $\mu_{c^{(i)}}$:$x^{(i)}$ 被分配给的聚类的中心。
则有代价函数作为优化目标:
$$J(c^{(1)}, … , c^{(m)}, \mu_1, … , \mu_K) = \frac{1}{m}\sum^m_{i=1} \| x^{(i)} - \mu_{c^{(i)}} \|^2$$
因此,K-means 算法就是要找到能使 $J(c^{(1)}, … , c^{(m)}, \mu_1, … , \mu_K)$ 最小的参数 $c^{(i)}$ 和 $\mu_K$。
随机初始化
一个更好的策略是不再从空间中随机选择点,而是从训练数据中随机选择以初始化聚类中心。
K-means 算法最终可能因为选取了不同的初始化点而收敛得到不同的结果。因此,可能落到局部最优。我们可以尝试多次随机初始化,并选择能够使代价函数最小的聚类结果。
选择聚类数量
通过改变 $K$ 值来得到一张代价函数下降的曲线图,并选择曲线的拐点的横坐标作为合适的 $K$ 值被称为“肘部法则(Elbow method)”,但不是所有时候得到的曲线都有明显的拐点。
降维
**降维(dimensionality reduction)**是指通过某种数学变换将原始高维属性空间转变为一个低维“子空间”,在这个子空间中样本密度大幅提高,以避免在高维情形下出现的数据样本稀疏、距离计算困难等问题。降维也是无监督学习问题的一种。
降维的两种应用:
- 数据压缩:对数据进行压缩,占用较少存储空间,并加速学习算法
- 数据可视化
主成分分析(PCA)
**主成分分析(Pricipal Component Analysis,PCA)**是最常用的一种降维算法。
PCA 会试图寻找一个低维的超平面,对数据进行投影,并最小化投影误差(数据点到该平面的距离)。在应用 PCA 之前,常规做法是先进行均值归一化和特征规范化。
输入样本集和降维后低维空间的维数 k 值,PCA 算法的过程为:
- 对所有样本进行中心化:$x_i \leftarrow x_i - \frac{1}{m}\sum^m_{i=1}x_i$ ;
- 计算样本的协方差矩阵 $XX^T$;
- 对协方差矩阵 $XX^T$ 做特征值分解;
- 取最大的 $k$ 个特征值所对应的特征向量 $w_1, w_2, …, w_k$。
则超平面 $W = (w_1, w_2, …, w_k)$。
选取 k 值
平均投影误差平方:
$$\frac{1}{m}\sum^m_{i=1} \| x^{(i)} - x^{(i)}_{approx} \|^2$$
数据的总方差:
$$\frac{1}{m}\sum^m_{i=1} \| x^{(i)} \|^2$$
因此选取较小的 k 值,使得:
$$\frac{\frac{1}{m}\sum^m_{i=1} \| x^{(i)} - x^{(i)}_{approx} \|^2}{\frac{1}{m}\sum^m_{i=1} \| x^{(i)} \|^2} \leq 0.01$$
这样,99% 的方差会被保留。
实现时,通常通过对协方差矩阵进行奇异值分解,将求得的特征值排序:$\lambda_1、\lambda_1、…、\lambda_m$,然后取 k 值使:
$$\frac{\sum^k_{i=1}S_{ii}}{\sum^m_{i=1}S_{ii}} \geq 0.99$$
压缩重现
$$z = U^T_{reduce}x$$
因此我们可以从低维数据重现一个近似的高维数据:
$$x \approx x_{approx} = U_{reduce}z$$
我们称这一过程为原始数据的重构(reconstruction)。
应用 PCA 的建议
用 PCA 可以降低数据的维度,从而使得算法运行更加高效。
- 从训练集中只抽取输入的向量,不要标签;
- 使用 PCA 得到原始数据的低维表示;
- 现在我们得到一个新的训练集。
注意:从 $x^{(i)}$ 到 $z^{(i)}$ 的映射需要通过**仅在训练集上运行 PCA **得到,不过这个映射关系同样可用于验证集和测试集。
一种错误的认知是可以使用 PCA 来防止过拟合。有些人会认为因为 PCA 能够降低数据维度,因此更少的特征数意味着更小的可能性导致过拟合。实际上,PCA 会舍弃一些有价值的信息,使用 PCA 来防止过拟合不是一种好的应用。使用正则化是更好的防止过拟合的方法。
在设计机器学习系统时,你可以先在原始数据上尝试运行算法,之后根据效果来决定是否使用 PCA 来加速学习或者压缩数据以减少所需的存储空间。
异常检测
**异常检测(Anomaly Detection)**是机器学习算法的一个常见应用。这是一个无监督学习问题,会通过新的数据特征落在已有数据的特征分布的概率来判断新的数据是否隐含了某种异常。
高斯分布
高斯分布(Gaussian ditribution),即正态分布(Normal ditribution)。
假设 $x \in \mathbb{R}$,如果 $x$ 的概率分布服从高斯分布,其中均值为 $\mu$,方差为 $\sigma^2$,则写作
$$x \sim \mathcal{N}(\mu, \sigma^2)$$
概率分布的公式为:
$$p(x;\mu, \sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})$$
参数估计(parameter estimation)问题是,给定数据集确定满足高斯分布,需要估计出 $\mu$ 和 $\sigma$。计算公式为:
$$\mu = \frac{1}{m}\sum^m_{i=1}x^{(i)}$$
$$\sigma^2 = \frac{1}{m}\sum^m_{i=1}(x^{(i)} - \mu)^2$$
其中,$\frac{1}{m}$ 有时也写作 $\frac{1}{m-1}$,在实践中区别不大。
算法
假设有一个训练集 $\big\{ x^{(1)},…,x^{(m)} \big\}$,每个样本 $x \in \mathbb{R}^n$。
在特征相互独立的假设下,有
$$p(x) = \prod^n_{j=1}p(x_j;\mu_j,\sigma_j^2)$$
如果 $p(x) < \varepsilon$,认为异常。$\varepsilon$ 需要选定。
分布项 $p(x)$ 的估计问题有时称为**密度估计(Density estimation)**问题。
开发和评估异常检测系统
如果有一些带标签的数据,来指明哪些是正常数据,哪些是异常数据,则这些数据可以用于评估算法。
我们这样划分训练集、验证集和测试集:
- 训练集:正常无标签数据
- 验证集和测试集:包含少量已知是异常的数据
系统开发步骤:
- 使用训练集拟合模型 $p(x)$;
- 对于验证集和测试集用模型进行预测;
- 因为数据类别比例相差较大,可以用 F1-Score 等来评估算法。
选择 $\varepsilon$ 的一种方法是使用多个值,最后选择能够最大化 F1-Score 的 $\varepsilon$ 值。
异常检测 VS 监督学习
异常检测与监督学习的区别:
- 异常检测中样本比例不平衡,而监督学习一般有比例相近的正负样本;
- 异常检测不追求从样本中分析出异常的具体种类,因为实际中可能出现与以前完全不同的全新异常。而监督学习会划分具体种类。
选择使用的特征
- 通过画直方图选择比较符合高斯分布的特征。不太符合的可以通过一些转换(例如取对数)使其符合高斯分布。
- 选择异常样本中值相对于正常样本概率较低的特征。这样,可以使异常样本得到相对较低的 $p(x)$。反映到实际中选择,可以是异常样本中某特征值异常地大或异常地校。
多元高斯分布
**多元高斯分布(Multivariate Gaussian distribution)**有两个参数 $\mu$ 和 $\Sigma$,$\mu \in \mathbb{R}$,$\Sigma \in \mathbb{R}^2$。
$$p(x;\mu, \Sigma) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp \Big( -\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu)\Big)$$
参数估计:
$$\mu = \frac{1}{m}\sum^m_{i=1}x^{(i)}$$
$$\Sigma = \frac{1}{m}\sum^m_{i=1}(x^{(i)}-\mu)(x^{(i)}-\mu)^T$$
使用原先的高斯分布的模型需要创建新的特征来捕捉异常的特征组合值。而多元高斯分布能够自动捕捉不同特征之间的关系;但原始模型的计算成本较低,可以使用数量巨大的特征。而多元高斯分布需要计算协方差矩阵 $Sigma$ 的逆矩阵,因此计算成本较高的同时,需要保证样本数量大于特征数量,来保证 $Sigma$ 可逆。
推荐系统
基于内容的推荐算法
一种做法是,我们将每部电影中爱情成分、动作成分等评值作为特征,而某用户对不同电影的打分作为标签。这样,为了做出预测,可以看作一个线性回归问题,对于用户 $j$,预测其给电影 $i$ 评分为 $(\theta^{(j)})^Tx^{(i)}$。
更正式的问题描述:

当学习 $\theta^{(1)}, \theta^{(2)}, \dots, \theta^{(n_u)}$ 时,优化目标为:
$$ \min_{\theta^{(1)},\dots,\theta^{(n_u)}} \frac{1}{2} \sum_{j=1}^{n_u} \sum_{i: r(i,j) = 1} \left( (\theta^{(j)})^T x^{(i)} - y^{(i,j)} \right)^2 + \frac{\lambda}{2} \sum_{j=1}^{n_u} \sum_{k=1}^{n} (\theta^{(j)}_k)^2 $$
通过梯度下降来更新参数:
当 $k=0$ 时: $$ \theta^{(j)}_k := \theta^{(j)}k - \alpha \sum{i: r(i,j) = 1} \left( (\theta^{(j)})^T x^{(i)} - y^{(i,j)} \right) x^{(i)}_k $$
当 $k \neq 0$ 时: $$ \theta^{(j)}_k := \theta^{(j)}k - \alpha \left( \sum{i: r(i,j) = 1} \left( (\theta^{(j)})^T x^{(i)} - y^{(i,j)} \right) x^{(i)}_k + \lambda \theta^{(j)}_k \right) $$ 两者的区别是因为一般不将偏置项 $b$ 计算在正则化项中。
协同过滤基本思想
实际上,获取电影的众多特征需要花费很高的人力。我们可以反向来思考这个问题,假设我们拥有了用户的偏好向量 $\theta^{(j)}$,为了学习 $x^{(i)}$,有:
$$min_{x^{(i)}}\frac{1}{2}\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum^n_{k=1}(x_k^{(i)})^2$$
学习 $x^{(1)}, x^{(2)}, …, x^{(n_u)}$ 时,则优化目标为:
$$min_{x^{(1)}, x^{(2)}, …, x^{(n_m)}}\frac{1}{2}\sum^{n_m}_{i=1}\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum^{n_m}_{i=1}\sum^n_{k=1}(x_k^{(i)})^2$$
这被称为协同过滤(Collaborative filtering)。
协同过滤算法
为了更高效地解得 $\theta$ 和 $x$,我们将两个代价函数合为一个:
$$J(x^{(1)}, x^{(2)}, …, x^{(n_u)}, \theta^{(1)}, \theta^{(2)}, … ,\theta^{(n_u)}) = \frac{1}{2}\sum_{(i,j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum^{n_m}_{i=1}\sum^n_{k=1}(x_k^{(i)})^2+ \frac{\lambda}{2}\sum^{n_m}_{i=1}\sum^n_{k=1}(x_k^{(i)})^2$$
$$min_{x^{(1)}, x^{(2)}, …, x^{(n_u)}, \theta^{(1)}, \theta^{(2)}, … ,\theta^{(n_u)}}J(x^{(1)}, x^{(2)}, …, x^{(n_u)}, \theta^{(1)}, \theta^{(2)}, … ,\theta^{(n_u)})$$
总结一下协同过滤算法:
- 将 $x^{(1)}, x^{(2)}, …, x^{(n_u)}, \theta^{(1)}, \theta^{(2)$ 初始化为较小的任意值;
- 用梯度下降来最小化 $J(x^{(1)}, x^{(2)}, …, x^{(n_u)}, \theta^{(1)}, \theta^{(2)}, … ,\theta^{(n_u)})$;
- 用某个用户的参数 $\theta$ 和某部电影的特征 $x$ 来预测他会给这部他没看过的电影打分为 $\theta^Tx$。
矢量化:低秩矩阵分解
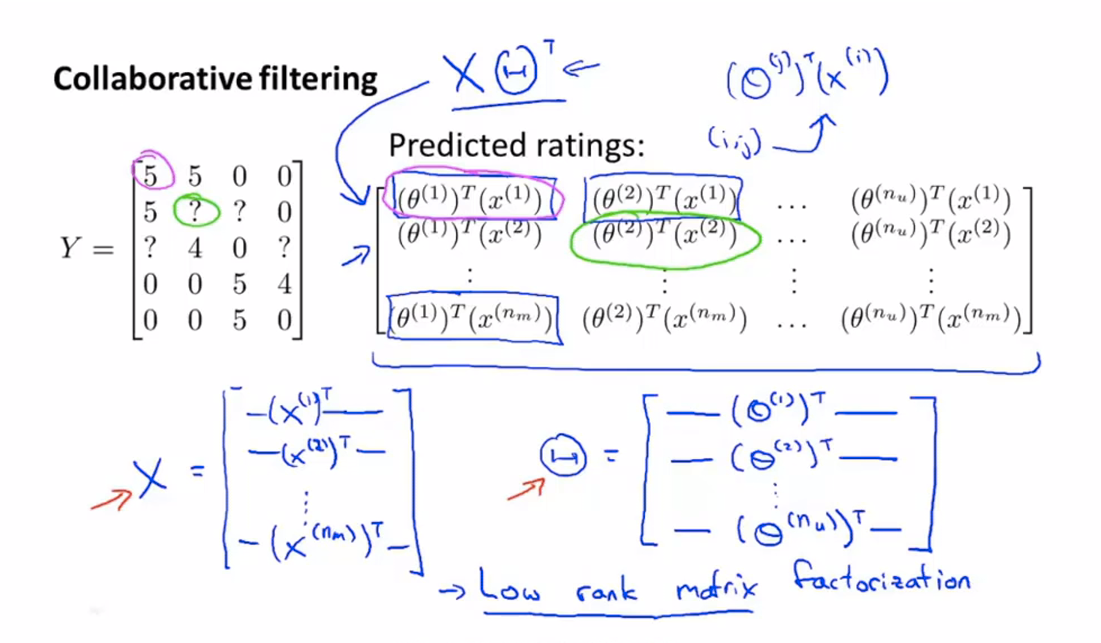
我们还可以通过特征来找到相关的电影,尽管这些特性可能不具有可解释性。
实施细节:均值规范化
对于一个新用户或者没有给任何电影评过分的用户,显然上述方法只会预测这名用户会给所有电影打 0 分。因此,我们要对每部电影的评分做一个均一化:

大规模机器学习
随机梯度下降
当我们每次使用全部的数据来进行梯度下降时,有公式:
$$\theta_j :=\theta_j - \alpha \frac{1}{m}\sum^m_{i=1}(h_{\theta}(x^{(i)}) - y^{(i)})x_j^{(i)}$$
每次求和的计算量太大,迭代速度慢,计算机的内存也可能不能支持所有数据。这种方法被称为批量梯度下降(Batch gradient descent)。
与此相对,有随机梯度下降(Stochastic gradient descent),在随机打乱所有数据后,每次只用一个训练数据来进行梯度下降以更新参数。这样,收敛速度更快。尽管这样做可能很难完全收敛,但可以非常接近全局最小值。
Mini-batch 梯度下降
Mini-batch 梯度下降每次迭代会使用 b 个样本。b 是一个称为 mini-batch 大小的参数,通常选取范围为 2 - 100。
使用 Mini-batch 梯度下降有时会比随机梯度下降有更快的收敛速度,这是因为在向量化后,可以合理使用并行运算。
每一个 Mini-batch 再计算一次 $J_{train}(\theta)$ 并和之前进行比对,可以确认梯度下降在正确执行,同时可以考虑将学习率调小使收敛更充分。
在线学习
**在线学习机制(Online learning setting)**可以支持有大量用户流的网站来快速调整模型,适应用户的喜好变化。每次将新鲜的用户数据用于梯度下降以调整参数,这些数据不用保存,用完即可丢弃。
MapReduce
MapReduce 指均分训练集,将每个子集分发给一台主机并行计算,最后结果汇总到一台机器,以加快计算速度。只要学习算法可以表示成一系列的求和形式,或者表示成在训练集上对函数的求和形式,就可以使用 MapReduce 技巧。把主机换成多核 CPU 的每个核同理。